Announcement
What Did Student Really Do?
(What Student Did, Part II)
When Student's t test for independent samples is run, every statistics
package reports two results. They may be labeled
| equal variances assumed |
equal variances not assumed |
| common variance |
separate variances |
| pooled variance |
separate variances |
Which results should be used?
The variances mentioned in the table and the output are
population variances. One thing Student did was to say that if
the population variances were known to be equal or could be assumed to be
equal, exact tests and confidence intervals could be obtained by using
his t distribution. This is the test labeled equal variances
assumed, common variance or pooled variance. The term
pooled variance refers to way the estimate of the common variance
is obtained by pooling the data from both samples.
The test labeled equal variances not assumed or separate
variances is appropriate for normally distributed individual values
when the population variances are known to be unequal or cannot be
assumed to be equal. This is not an exact test. It is approximate. The
approximation involves t distributions with non-integer degrees of
freedom. Before the ready availability of computers, the number of
degrees of freedom was awkward to calculate and the critical values were
not easy to obtain, so statisticians worried about how much the data
could depart from the ideal of equal variances without affecting the
validity of Student's test. It turned out the t test was extremely
robust to departures from normality and equal variances.
Some analysts recommended performing preliminary statistical tests to
decide whether the data were normally distributed and whether population
variances were equal. If the hypothesis of equal population variances
was rejected, the equal variances not assumed form of the test
would be used, otherwise equal variances assumed version would be
used. However, it was discovered that Students t test for independent
samples was so robust that the preliminary tests would have analysts
avoiding the equal variances assumed form when it was in no danger
of it giving misleading results. These preliminary tests often detect
differences too small to affect Student's t test. The analogy most often
given is that using preliminary tests of normality and equality of
variances to decided whether it was safe to use the equal variances
assumed version of the t test was like sending out a rowboat to see
whether it was safe for the ocean liner. Today, common practice is to
avoid preliminary tests. Important violations of the requirements will
be detectable to the naked eye without a formal significance test.
Rupert Miller, Jr., in his 1986 book Beyond ANOVA, Basics of
Applied Statistics, {New York: John Wiley & Sons] summarizes the
extent to which the assumptions of normality and equal population
variances can be violated without affecting the validity of Student's
test.
- If sample sizes are equal, (a) nonnormality is not a problem and (b)
the t test can tolerate population standard deviation ratios of 2 without
showing any major ill effect. The worst situation occurs when one sample
has a much larger variance and a much smaller sample size than the other.
For example, if the variance ratio is 5 and the sample size ratio is 1/5,
a nominal P value of 0.05 is actually 0.22.
- Serious distortion of the P value can occur when the skewness of the
two populations is different.
- Outliers can distort the mean difference and the t statistic. They
tend to inflate the variance and depress the value and corresponding
statistical significance of the t statistic.
Still, which test should be used?
Frederick Mosteller and John Tukey, on pages 5-7 of Data Analysis
and Regression [Reading, MA: Addison-Wesley Publishing Company, Inc.,
1997] provide insight into what Student really did and how it should
affect our choice of test.
The value of Student's work lay not in great numerical change, but in:
- recognition that one could, if appropriate assumptions held, make
allowances fo the "uncertainties" of small samples, not only in Student's
original problem, but in others as well;
- provision of a numerical assessment of how small the necessary
numerical adjustment of confidence points were in Student's problem...
- presentation of tables that could be used--in setting confidence
limits, in making significance tests--to assess the uncertainty
associated with even very small samples.
Besides its values, Student's contribution had its drawbacks, notably:
- it made it too easy to neglect the proviso "if appropriate
assumptions held";
- it overemphasized the "exactness of Student's solution for his
idealized problem";
- it helped to divert the attention of theoretical statisticians to the
development of "exact" ways of treating other problems; and
- it failed to attack the "problem of multiplicity": the difficulties
and temptation associated with the application of large numbers of tests
to the same data.
The great importance given to exactness of treatment is even more
surprising when we consider how much the small differences between the
critical values of the normal approximation and Student's t
disappears, especially at and near the much-used two-sided 5% point,
when, as suggested by Burrau (1943), we multiply t by the constant
required to bring its variance to 1, namely, [ 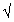 {(f - 2) /f}].
{(f - 2) /f}].
The separate variances version rarely differs from common variance.
When it does, there's usually a problem with the common variances
version.
When sample sizes are large, the Central Limit Theorem takes over.
The behavior of the separate variances t statistic is described by the
normal distribution regardless of the distribution of the individual
observations. The two populations of individual observations need not
have the same variances. They need not even be normal.
If the separate variances t test is always valid for large samples and
if the common variances test is probably invalid when the two tests
disagree in small samples, why not use the separate variances version
exclusively? Some statisticians seem to advocate this approach. The
primary advantage of the common variances test is that it generalizes to
more than two groups (analysis of variance).
When within group variances are unequal, it often happens that the
standard deviation is proportional to the mean. For example, instead of
the within group standard deviation being a fixed value such as 5 mg/dl,
it is often a fixed percentage. If the standard deviation were 20% of
the mean, one group might have values of 10 give or take 2, while the
other might have values of 100 give or take 20. In such cases, a
logarithmic transformation will produce groups with the same standard
deviation. If natural logarithms are use, the common within group
standard deviation of the transformed data will be equal to the ratio of
the within group standard deviation to the mean (also known as the
coefficient of variation).
The purpose of transforming data is not to achieve a particular
result. Transformations are not performed to make differences achieve
statistical significance. Transformations allow us to use standard
statistical techniques confident they are appropriate for the data to
which they're applied. That is, transformations are applied not to
achieve a particular result, but to insure the results we obtain will be
reliable.
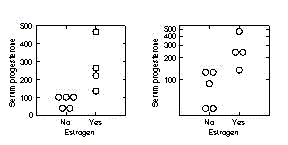 The following
small dataset illustrates some of the issues. Serum progesterone levels
were measured in subjects randomized to receive estrogen or not. The
group with the higher serum progesterone levels also has the greater
spread. The equal variances assumed t test has an observed significance
level of 0.022; the unequal variances assumed t test has an observed
significance level of 0.069. When a (natural) logarithmic transformation
(ln) is applied to the data, the within group standard deviations are
both around 0.50, which is approximately the ratio of the SD to the mean,
and both P values are 0.012. The conclusion is that the geometric mean
of progesterone levels of those given this dose of progesterone is
between 1.4 and 7.9 times the levels of those on placebo (95% CI).
Insofar as the geometric mean is a good approximation to the median, the
previous sentence might be restated in terms of medians.
The following
small dataset illustrates some of the issues. Serum progesterone levels
were measured in subjects randomized to receive estrogen or not. The
group with the higher serum progesterone levels also has the greater
spread. The equal variances assumed t test has an observed significance
level of 0.022; the unequal variances assumed t test has an observed
significance level of 0.069. When a (natural) logarithmic transformation
(ln) is applied to the data, the within group standard deviations are
both around 0.50, which is approximately the ratio of the SD to the mean,
and both P values are 0.012. The conclusion is that the geometric mean
of progesterone levels of those given this dose of progesterone is
between 1.4 and 7.9 times the levels of those on placebo (95% CI).
Insofar as the geometric mean is a good approximation to the median, the
previous sentence might be restated in terms of medians.
The analysis is presented in the common log scale (log), also. All
test statistics and signifcance levels from the two log transformed
analyses are identical. The numerical values of the summary statistics
such as mean, SD, and confidence intervals differ, but are equivalent.
The equivalence can be seen by taking the appropriate anti-logarithm of
each number. For example, the mean value of log(SPROG) in the
Estrogen group is 2.3917 while the mean value of ln(SPROG) is
5.5072, but both 102.3917 and e5.5072 are
equal to 246.4. The within-group SD is equal to the coefficient of
variation for the natural log transformation only.
This is a very small dataset, so small that tests for the inequality
of population variances do not achieve statistical significance, even
though one SD is three times larger than the other. Still,
it possesses the essential features of one group having a much larger
standard deviation and the standard deviations being proportional to mean
response, so it is worthy of consideration.
|
Estrogen
|
N
|
Mean
|
SD
|
SEM
|
|
SPROG
|
No
|
5
|
81.8000
|
40.4747
|
18.1008
|
|
Yes
|
4
|
271.5000
|
139.5337
|
69.7669
|
|
ln(SPROG)
|
No
|
5
|
+
4.2875
|
.5617
|
.2512
|
|
Yes
|
4
|
5.5072
|
.5076
|
.2538
|
|
log(SPROG)
|
No
|
5
|
1.8620
|
.2439
|
.1091
|
|
Yes
|
4
|
2.3917
|
.2204
|
.1102
|
|
|
Levene's Test for Equality of
Variances |
t-test for Equality of
Means
|
|
|
95% Confidence Interval
of the Difference
|
|
|
F
|
Sig.
|
t
|
df
|
Sig. (2-tailed)
|
Mean Difference
|
Std. Error Difference
|
Lower
|
Upper
|
|
SPROG
|
Equal variances assumed
|
2.843
|
.136
|
-2.935
|
7
|
.022
|
-189.7000
|
64.6229
|
-342.5088
|
-36.8912
|
|
Equal variances not assumed
|
|
|
-2.632
|
3.406
|
.069
|
-189.7000
|
72.0767
|
-404.3650
|
24.9650
|
|
ln(SPROG)
|
Equal variances assumed
|
.639
|
.450
|
-3.372
|
7
|
.012
|
-1.2197
|
.3617
|
-2.0750
|
-.3644
|
|
Equal variances not assumed
|
|
|
-3.416
|
6.836
|
.012
|
-1.2197
|
.3571
|
-2.0682
|
-.3712
|
|
log(SPROG)
|
Equal variances assumed
|
.639
|
.450
|
-3.372
|
7
|
.012
|
-.5297
|
.1571
|
-.9012
|
-.1583
|
|
Equal variances not assumed
|
|
|
-3.416
|
6.836
|
.012
|
-.5297
|
.1551
|
-.8982
|
-.1612
|
Gerard E.
Dallal
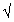 {(f - 2) /f}].
{(f - 2) /f}].
 The following
small dataset illustrates some of the issues. Serum progesterone levels
were measured in subjects randomized to receive estrogen or not. The
group with the higher serum progesterone levels also has the greater
spread. The equal variances assumed t test has an observed significance
level of 0.022; the unequal variances assumed t test has an observed
significance level of 0.069. When a (natural) logarithmic transformation
(ln) is applied to the data, the within group standard deviations are
both around 0.50, which is approximately the ratio of the SD to the mean,
and both P values are 0.012. The conclusion is that the geometric mean
of progesterone levels of those given this dose of progesterone is
between 1.4 and 7.9 times the levels of those on placebo (95% CI).
Insofar as the geometric mean is a good approximation to the median, the
previous sentence might be restated in terms of medians.
The following
small dataset illustrates some of the issues. Serum progesterone levels
were measured in subjects randomized to receive estrogen or not. The
group with the higher serum progesterone levels also has the greater
spread. The equal variances assumed t test has an observed significance
level of 0.022; the unequal variances assumed t test has an observed
significance level of 0.069. When a (natural) logarithmic transformation
(ln) is applied to the data, the within group standard deviations are
both around 0.50, which is approximately the ratio of the SD to the mean,
and both P values are 0.012. The conclusion is that the geometric mean
of progesterone levels of those given this dose of progesterone is
between 1.4 and 7.9 times the levels of those on placebo (95% CI).
Insofar as the geometric mean is a good approximation to the median, the
previous sentence might be restated in terms of medians.