 0
+
0
+  1 DUR
+
1 DUR
+  2 M0F1
+
2 M0F1
+ 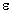
This note considers the case of multiple linear regression with two predictors, where one of the predictors is an indicator variable. It will be coded 0/1 here, but these results do not depend on the the two values used. Here, men and women are placed on a treadmill. When they can no longer continue, duration (DUR) and maximum oxygen usage (VO2max) are recorded. The purpose of this analysis is to predict VO2max from sex (M0F1 = 0 for males, 1 for females) and DUR. When the model
 0
+
0
+  1 DUR
+
1 DUR
+  2 M0F1
+
2 M0F1
+ 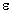
 When the data are plotted in
three dimensions, it is seen that they lie along two slices--one slice
for each of the two values of M0F1. The regression surface is once
again a flat plane. This follows from our choice of a model.
When the data are plotted in
three dimensions, it is seen that they lie along two slices--one slice
for each of the two values of M0F1. The regression surface is once
again a flat plane. This follows from our choice of a model.
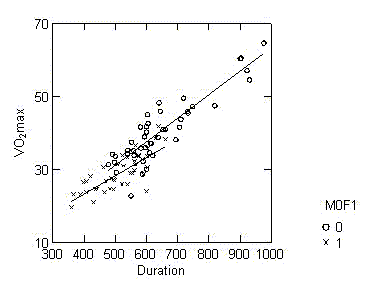
 The data in each
slice can be plotted as VO2max against DUR and the two plots can be
superimposed. The two lines are the pieces of the plane corresponding to
M0F1=0 and M0F1=1. The lines are parallel because they are parallel
strips from the same flat plane. This also follow directly from the
model. The fitted equation can be rewritten conditional on the two values
of M0F1. When M0F1=0, the model is
The data in each
slice can be plotted as VO2max against DUR and the two plots can be
superimposed. The two lines are the pieces of the plane corresponding to
M0F1=0 and M0F1=1. The lines are parallel because they are parallel
strips from the same flat plane. This also follow directly from the
model. The fitted equation can be rewritten conditional on the two values
of M0F1. When M0F1=0, the model is
 A more complicated
model can be fitted that does not force the lines to be parallel. This
is discussed in the note on interactions. Those
lines are fitted in the picture to the left. The test for
whether the lines are parallel has an observed significance level of
0.102. Thus, the regression coefficients are within sampling variability
of each other and the lines are within sampling variability of what one
would expect of parallel lines. In general, we like simpler models (in
keeping with Occam's Razor: Use the simplest model that is consistent
with the data.) because they are more easily described. The parallel
slopes model says that men are expected to have a VO2max 3.4623 units higher
than women who last on the treadmill for the same DURation. When the lines
are not parallel, the expected difference in VO2max between a male and female
with the same DURation depends on the value of DURation. In the picture to the
left, the expected difference in VO2max increases with DURation. However, as
already noted, there is not enough evidence to claim that this change in
difference is real.
A more complicated
model can be fitted that does not force the lines to be parallel. This
is discussed in the note on interactions. Those
lines are fitted in the picture to the left. The test for
whether the lines are parallel has an observed significance level of
0.102. Thus, the regression coefficients are within sampling variability
of each other and the lines are within sampling variability of what one
would expect of parallel lines. In general, we like simpler models (in
keeping with Occam's Razor: Use the simplest model that is consistent
with the data.) because they are more easily described. The parallel
slopes model says that men are expected to have a VO2max 3.4623 units higher
than women who last on the treadmill for the same DURation. When the lines
are not parallel, the expected difference in VO2max between a male and female
with the same DURation depends on the value of DURation. In the picture to the
left, the expected difference in VO2max increases with DURation. However, as
already noted, there is not enough evidence to claim that this change in
difference is real.