|
Sum of Squares |
Degrees of Freedom |
|
| A |  |
a-1 |
| B |  |
b-1 |
| AB |  |
(a-1)(b-1) |
| Residual |  |
(n-1)ab |
| Total |  |
nab-1 |
Analysis of Variance is a set of techniques for studying means. It works by looking at the variability in a response variable, breaking the variability apart, and assigning pieces to different effects. Consider the analysis of a balanced two-factor study where the common cell count is n.
|
Sum of Squares |
Degrees of Freedom |
|
| A |  |
a-1 |
| B |  |
b-1 |
| AB |  |
(a-1)(b-1) |
| Residual |  |
(n-1)ab |
| Total |  |
nab-1 |
For both sums of squares and degrees of freedom, Total=A+B+AB, that is the total variability in the data set is partitioned into three pieces. One piece describes how the row means differ from each other. Another describes how the column means differ from each other. The third describes the extent to which the row and column effects are not additive.
Each piece of the variability is associated with a particular piece of the ANOVA model
 +
+  i +
i +  j + (
j + (
 )ij +
)ij + 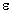 ij
ij The following dicussion of pooling is an immediate consequence of a few facts.
Pooling
The idea behind pooling is that any effect that is not statistically significant can be eliminated from the model and the model can be refitted. In that case, the sums of squares and degrees of freedom corresponding to the eliminated terms are added into the residual sum of squares and degrees of freedom.
The first question should be, "Why bother?! What does it gain?" Primarly, residual degrees of freedom. This can help if the residual degrees of freedom for the full model is small--less than 10 or 20, say. In most studies, however, this is not an issue.
Pooling is a bad idea because the decision whether to pool is based on looking at the data. Any time the decision whether to do something is based on looking at the data, P values end up being different from what was originally though. Simulation studies have shown what might be expected. If the absence of an effect were known beforehand, pooling would be automatic regardless of the F ratio for the effect. In practice, pooling takes only after the mean squares for effects being pooled are seen not to be large compared to the original Residual Mean Square. When their sums of squares and degrees of freedom are combined with those of the original Residual, the new Residual mean squares is typically smaller than it would be if there were no peeking allowed. This has the effect of making ratios with this new Residual Mean Square in the denominator larger than they should be and other effects are more likely to appear statistically significant.
Other issues
More important than pooling is the notion that effects that do not appear in the model get folded into the residual sum of squares. Consider a two factor experiment once again. To keep things simple, let both factors have two levels. The issues surrounding pooling illustrate why it is inappropriate to use a simple t test to test the main effects even in the absence of an interaction.
 In the diagram to the left, the
levels of Factor A ar indicated by the tick marks on the horizontal axis.
The levels of factor B are indicated by a 'o' or '+'. The reponse is
higher for level 'o' of Factor B. The difference between 'o' and '+' is
not significantly different for A1 and A2
(interaction P = 0.152). If Student's t test for independent samples is
used to compare the levels of A--that is, if the presence of factor B is
ignored--the P value is 0.109. However, in a two-factor analysis of
variance, the P value for the main effect of Factor A is <0.001.
In the diagram to the left, the
levels of Factor A ar indicated by the tick marks on the horizontal axis.
The levels of factor B are indicated by a 'o' or '+'. The reponse is
higher for level 'o' of Factor B. The difference between 'o' and '+' is
not significantly different for A1 and A2
(interaction P = 0.152). If Student's t test for independent samples is
used to compare the levels of A--that is, if the presence of factor B is
ignored--the P value is 0.109. However, in a two-factor analysis of
variance, the P value for the main effect of Factor A is <0.001.
Both tests look at the same mean difference in levels of Factor A. The reason the P values are so different is the variabilty against which the mean difference is compared. In the t test, it is compared to the pooled estimate of variability within a strip of observations defined by the tick marks (2.75). In the two factor ANOVA, it is compared to the pooled estimate of within cell variability (0.98). The estimate of variability used for the t test is so much larger because it overlooks the Factor B effect. Variabilty that could be assigned to Factor B is left in the Residual Sum of Squares, inflating it. Both analyses follow, with the t test presented as a single factor ANOVA to make the visual comparison easier.
Source Sum of df Mean F-ratio P Squares Square A 19.828 1 19.828 2.617 0.109 Error 742.488 98 7.576 Total 762.316 99 ----------------------------------------------- A 19.828 1 19.828 20.553 0.000 B 647.858 1 647.858 671.542 0.000 A*B 2.016 1 2.016 2.090 0.152 Error 92.614 96 0.965 Total 762.316 99
The same principle applies to every regression analysis. Whenever a potential eplanatory variable is overlooked, its explanatory capability remains in the residual sum of squares. In this balanced ANOVA example, the sums of squares were additive because balance makes the effects uncorrelated. In the general regression problem predictors will be correlated. The various sums of squares--each variable adjusted for the presence of the others--will not be exactly additive, but the residual sum of squares will be inflated to the extent to which important predictor variables not appearing in the model are not perfectly correlated with the predictors in the model.