| Diet Record |
Food Frequency Questionnaire |
Count |
|---|---|---|
| <RDA | <RDA | 33 |
| <RDA | 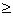 RDA RDA |
27 |
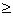 RDA RDA |
<RDA | 13 |
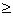 RDA RDA |
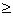 RDA RDA |
44 |
Paired Counts
Gerard E. Dallal, Ph.D.
There are as many ways to collect paired counts as there are reasons for measuring something twice. Subjects might be classified into one of two categories according to two different measuring devices. Opinions (pro and con) might be assessed before and after some intervention. Just as it was necessary account for pairing when analyzing continuous data--choosing Student's t test for paired samples rather than the test for independent samples--it is equally important to take account of pairing when analyzing counts.
Consider a study to examine whether food frequency questionnaires and three-day food diaries are equally likely to label a women as consuming less than the RDA of calcium. One way to conduct this study is to take a sample of women and assign them at random to having their calcium intake measured by food frequency or diary. However, calcium intake can vary considerably from person to person, so a better approach might be to use both instruments to evaluate a single sample of women.
Suppose this latter approach is taken with a sample of 117 women and the results are as follows:
| Diet Record |
Food Frequency Questionnaire |
Count |
|---|---|---|
| <RDA | <RDA | 33 |
| <RDA | 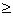 RDA RDA |
27 |
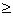 RDA RDA |
<RDA | 13 |
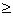 RDA RDA |
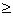 RDA RDA |
44 |
How should the data be analyzed? Pearson's test for homogeneity of proportions comes to mind and it is tempting to construct the table
| Calcium Intake | ||
|---|---|---|
| <RDA | 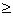 RDA RDA |
|
| Food Frequency Questionnaire |
46 | 71 |
| Diet Record | 60 | 57 |
However, there are some problems with this approach.
Here's another way to represent the data in which each subject appears once and only once.
| Diet Records |
Food Frequency Questionnaire |
|
|---|---|---|
| <RDA | 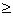 RDA RDA |
|
| <RDA | 33 | 27 |
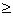 RDA RDA |
13 | 44 |
However, even though each person appears only once, you have to resist the urge to use Pearson's goodness-of-fit test because it tests the wrong hypothesis!
The question is still whether the two instruments identify the same proportion of women as having calcium intakes below the RDA. The Pearson goodness-of-fit statistic does not test this. It tests whether the classification by food frequency is independent of the classification by Diet Record!
[These are two different things! Consider the following table.
Diet
RecordsFood Frequency
Questionnaire<RDA RDA
<RDA 20 20 RDA
10 10 The two instruments are independent because half of the subjects' intakes are declared inadequate by the FFQ regardless of what the Diet Record says. Yet, while the FFQ says half of the subjects (30 out of 60) have inadequate intake, the Diet Record says two-thirds (40 out of 60) of the intakes are inadequate.]
There may be cases where you want to test for independence of the two instruments. Those who have little faith in either the Diet Record or Food Frequency Questionnaire might claim that the test is appropriate in this case! But, usually you already know that the methods agree to some extent. This makes a test of independence pointless.
The appropriate test in this situation is known as McNemar's test. It is based on the observation that if the two proportions are equal, then discordant observations (where the methods disagree) should be equally divided between (low on frequency, high on diary) and (high on frequency, low on diary). Some commonly used test statistics are
where b and c are the discordant cells in the 2 by 2 table. Both of statistics are referred to the chi-square distribution with 1 degree of freedom. Since the test statistics involve the square of the difference between the counts, they are necessarily two-sided tests (For these data: X1 = 4.90, P = 0.0269; X2 = 4.23, P = 0.0397.)
While it may seem strange, counter-intuitive, and even wrong when the realization first hits, the only relevant data are the numbers in the discordant cells, here the 27 and the 13. The information about how diet records and FFQs disagree is the same whether the cell counts showing agreement are 33 and 44 or 33,000,000 and 44,000,000. The distinction is that in this lattercase a statistically significant difference may be of no practical importance.
Other situations in which McNemar's test is appropriate include measuring change (status before and after an intervention) and case- control studies in which everyone is measured for the presence/absence of a characteristic. The feature that should sensitize you to McNemar's test is that both measurements are made on the same observational unit, whether it be an individual subject or case-control pair.
[back to The Little Handbook of
Statistical Practice]