Announcement
Proportions
This is another way of looking at the content of the Contingency
Tables page when two-by-two contingency tables are used to compare
two proportions. This approach appears in almost every introductory
statistics text. It's easily understood, and it shows how the analysis
of proportions is nearly the same as the analysis of means, despite the
difference in appearance.
[Notation: The obvious notational choice for proportion or probability
is p. The standard convention is to use Roman letters for sample
quantities and the corresponding Greek letter for population quantities.
Some books do just that. However, the Greek letter  has its own special place in mathematics.
Therefore, instead of using pfor sample proportion and
has its own special place in mathematics.
Therefore, instead of using pfor sample proportion and  for population proportion, many authors use
p for population proportion and p with a hat (caret) on
it,
for population proportion, many authors use
p for population proportion and p with a hat (caret) on
it, 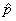 (called p-hat), as the
sample proportion. The use of "hat" notation for differentiating between
sample and population quantities is quite common.]
(called p-hat), as the
sample proportion. The use of "hat" notation for differentiating between
sample and population quantities is quite common.]
Confidence Intervals
There's really nothing new to learn to compare two proportions because
we know how to compare means. Proportions are just means! The
proportion having a particular characteristic is the number of
individuals with the characteristic divided by total number of
individuals. Suppose we create a variable that equals 1 if the subject
has the characteristic and 0 if not. The proportion of individuals with
the characteristic is the mean of this variable because the sum of these
0s and 1s is the number of individuals with the characteristic.
While it's never done this way (I don't know why not*), two
proportions could be compared by using Student's t test for independent
samples with the new 0/1 variable as the response.
An approximate 95-% confidence interval for the difference between
two population proportions (p1-p2) based on two
independent samples of size n1 and n2 with sample
proportions 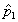 and
and 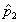 is given by
is given by

Even though this looks different from other formulas we've seen, it's
nearly identical to the formula for the "equal variances not assumed"
version of Student's t test for independent samples. The only difference
is that the SDs are calculated with n in the
denominator instead of n-1.
An approximate 95-% confidence interval for a single population
proportion based on a sample of size n with sample proportion 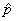 is
is

Significance Tests
Comparing Two Proportions
There is a choice of test statistics for testing the null hypothesis
H0: p1=p2 (the population proportions
are equal) against H1: p1 p2 (the population proportions are
not equal). The test is performed by calculating one of these statistics
and comparing its value to the percentiles of the standard normal
distribution to obtain the observed significance level. If this P value
is sufficiently small, the null hypothesis is rejected.
p2 (the population proportions are
not equal). The test is performed by calculating one of these statistics
and comparing its value to the percentiles of the standard normal
distribution to obtain the observed significance level. If this P value
is sufficiently small, the null hypothesis is rejected.
Which statistic should be used? Many statisticians have offered
arguments for preferring one statistic over the others but, in practice,
most researchers use the one that is provided by their statistical
software or that is easiest to calculate by hand.
All of the statistics can be justified by large sample statistical
theory. They all reject H0 100(1- )% of the time when H0is true.
(However, they don't always agree on the same set of data.) Since they
all reject H0 with the same frequency when it is true, you
might think of using the test that is more likely to reject H0
when it is false, but none has been shown to be more likely than the
others to reject H0 when it is false for all alternatives to
H0.
)% of the time when H0is true.
(However, they don't always agree on the same set of data.) Since they
all reject H0 with the same frequency when it is true, you
might think of using the test that is more likely to reject H0
when it is false, but none has been shown to be more likely than the
others to reject H0 when it is false for all alternatives to
H0.
The first statistic is
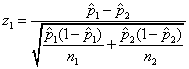 ,
,
The second is
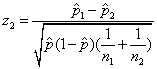 ,
,
where 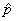 is the proportion of
individuals having the characteristic when the two samples are lumped
together.
is the proportion of
individuals having the characteristic when the two samples are lumped
together.
A third statistic is

The test statistic z1 is consistent with the
corresponding confidence interval, that is, z1 rejects
H0 at level  if and only if
the 100(1-
if and only if
the 100(1- )% confidence interval does
not contain 0.
)% confidence interval does
not contain 0.
The test statistic z2 is equivalent to the chi-
square goodness-of-fit test, also called (correctly) a test of
homogeneity of proportions and (incorrectly, for this application) a test
of independence.
The test statistic z3 is equivalent to the chi-
square test with Yates's continuity correction. It was developed to
approximate another test statistic (Fisher's exact test) that was
difficult to compute by hand. Computers easily perform this calculation,
so this statistic is now obsolete. Nevertheless, most statistical program
packages continue to report it as part of their analysis of proportions.
Examples
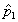 =8/13 and
=8/13 and 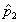 =3/13. Then, z1=2.155 (P=0.031),
z2=1.985 (p=0.047), and z3=1.588 (P=0.112).
Fisher's exact test gives P=0.111.
=3/13. Then, z1=2.155 (P=0.031),
z2=1.985 (p=0.047), and z3=1.588 (P=0.112).
Fisher's exact test gives P=0.111.
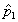 =16/34 and
=16/34 and 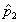 =6/26. Then, z1=2.016
(P=0.044) and z2=1.910 (p=0.056). A 95% CI for p1-p2 is
0.2398
=6/26. Then, z1=2.016
(P=0.044) and z2=1.910 (p=0.056). A 95% CI for p1-p2 is
0.2398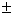 0.2332=(0.0066,0.4730). The
confidence interval agrees with z1. The CI does not contain
0, while z1 rejects H0:
p1=p2. However, z1 and the CI disagree
with z2 which fails to reject H0.
0.2332=(0.0066,0.4730). The
confidence interval agrees with z1. The CI does not contain
0, while z1 rejects H0:
p1=p2. However, z1 and the CI disagree
with z2 which fails to reject H0.
Common sense suggests using z1 because it avoids
conflicts with the corresponding confidence interval. However, in
practice, the chi-square test for homogeneity of proportions (equivalent
to z2) is used because that's what statistical software
packages report. I don't know any that report z1. However,
z2 (in the form of the chi-square test) has the advantage of
generalizing to tests of the equality of more than two proportions.
Tests Involving a Single Population Proportion
When testing the null hypothesis H0: the population
proportion equals some specified value p0 against
H1: the population proportion does not equal p0,
there is, once again, a choice of test statistics.

all of which are compared to the percentiles of the standard
normal distribution.
Again, z1 gives tests that are consistent with the
corresponding confidence intervals, z2 is equivalent to the
chi-square goodness-of-fit test, and z3 gives one-sided P-
values that usually have better agreement with exact P-values obtained,
in this case, by using the binomial distribution.
Comment
These techniques are based on large sample theory. Rough rules of
thumb say they may be applied when there are at least five occurrences of
each outcome in each sample and, in the case of a single sample, provided
confidence intervals lie entirely in the range (0,1).
Summary
- We can construct confidence intervals for population proportions and
for the difference between population proportions just as we did for
population means.
- We can test the hypothesis that two population proportions are equal
just as we did for population means.
- The formulas for constructing confidence intervals and for
testing the hypothesis of equal proportions are slightly
different, unlike the case of means where the two formulas are the same.
- As a consequence of (3), it is possible (although uncommon) for the
test to reject the hypothesis of equal proportions while the CI for their
difference contains 0, or for the test to fail to reject while the CI
does not contain 0!
- The formula for CIs can be adapted for significance testing.
However, the formula for significance tests cannot be adapted for
constructing CIs.
- Which test statistic should be used? All are equally valid. Almost
every statistical program provides a test procedure that is equivalent to
z2 for comparing proportions, so that's what people use.
- Why is the test statistic based on the CI for
population differences not widely available in statistical
software? Because the chi-square test is easily generalized
to classifications with more than two categories. The other
test statistic is not.
- This is just the tip of the iceberg. When the
response is counts, there can be dozens of valid test
statistics and methods for constructing confidence intervals,
all giving slightly different results. The good news is that
they tend to give the same inference (lead to the same
conclusion).
Copyright © 2000 Gerard
E. Dallal
 has its own special place in mathematics.
Therefore, instead of using pfor sample proportion and
has its own special place in mathematics.
Therefore, instead of using pfor sample proportion and  for population proportion, many authors use
p for population proportion and p with a hat (caret) on
it,
for population proportion, many authors use
p for population proportion and p with a hat (caret) on
it, 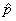 (called p-hat), as the
sample proportion. The use of "hat" notation for differentiating between
sample and population quantities is quite common.]
(called p-hat), as the
sample proportion. The use of "hat" notation for differentiating between
sample and population quantities is quite common.]
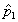 and
and 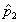 is given by
is given by 
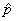 is
is 
 p2 (the population proportions are
not equal). The test is performed by calculating one of these statistics
and comparing its value to the percentiles of the standard normal
distribution to obtain the observed significance level. If this P value
is sufficiently small, the null hypothesis is rejected.
p2 (the population proportions are
not equal). The test is performed by calculating one of these statistics
and comparing its value to the percentiles of the standard normal
distribution to obtain the observed significance level. If this P value
is sufficiently small, the null hypothesis is rejected.  )% of the time when H0is true.
(However, they don't always agree on the same set of data.) Since they
all reject H0 with the same frequency when it is true, you
might think of using the test that is more likely to reject H0
when it is false, but none has been shown to be more likely than the
others to reject H0 when it is false for all alternatives to
H0.
)% of the time when H0is true.
(However, they don't always agree on the same set of data.) Since they
all reject H0 with the same frequency when it is true, you
might think of using the test that is more likely to reject H0
when it is false, but none has been shown to be more likely than the
others to reject H0 when it is false for all alternatives to
H0.
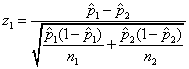 ,
,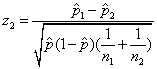 ,
,
 0.2332=(0.0066,0.4730). The
confidence interval agrees with z1. The CI does not contain
0, while z1 rejects H0:
p1=p2. However, z1 and the CI disagree
with z2 which fails to reject H0.
0.2332=(0.0066,0.4730). The
confidence interval agrees with z1. The CI does not contain
0, while z1 rejects H0:
p1=p2. However, z1 and the CI disagree
with z2 which fails to reject H0.