The sample mean plays many distinct roles.

• It is the best estimate of an individual value in the sample. ("If I were to select one observation at random from the sample, what would you guess that value to be?" "<The sample mean>.")
• It is the best estimate of an individual value drawn from the population. ("If I were to select one observation from the population, what would you guess that value to be?" "<The sample mean>." Or, "If we were to collect one more observation, what would you guess its value to be?" "<The sample mean>.") Notice that collecting one more observation is the same thing as drawing an observation at random from the population.
• It is the best estimate of the mean of the population from which the sample was drawn. ("What would you guess the mean of all values in the population to be?" "<The sample mean>.")
• Whatever else it is, it is the mean of the sample.

The sample mean and standard deviation (, s) together summarize individual data values when the data follow a normal distribution or something not too far from it. The sample mean describes a typical value. The sample standard deviation (SD) measures the spread of individual values about the sample mean. The SD also estimates the spread of individual values about the population mean teh extent to which a single value chosen at random might differ from the population mean.

Just as the sample standard deviation measures the uncertainty with which the sample mean estimates individual measurements, a quantity called the Standard Error of the Mean (SEM = ) measures the uncertainty with which the sample mean estimates a population mean. Read the last sentence again...and again.

• The sample mean estimates individual values.
  • The uncertainty with which  estimates individual values is given by the SD.
• The sample mean estimates the population mean.
  • The uncertainty with which  estimates the population mean is given by the SEM.

Intuition says the more data there are, the more accurately we can estimate a population mean. With more data, the sample and population means are likely to be closer. The SEM expresses this numerically. The SEM says the likely difference between the sample and population means, , decreases as the sample size increases, but the decrease is proportional to the square root of the sample size. To decrease the uncertainty by a factor of 2, the sample size must be increased by a factor of 4; to cut the uncertainty by a factor of 10, a sample 100 times larger is required.

We have already noted that when individual data items follow something not very far from a normal distribution, 68% of the data will be within one standard deviation of the mean, 95% will be within two standard deviations of the mean, and so on. But, this is true only when the individual data values are roughly normally distributed.

There is an elegant statistical limit theorem that describes the likely difference between sample and population means, , when sample sizes are large. It is so central to statistical practice that is is called the Central Limit Theorem. It says that, for large samples, the normal distribution can be used to describe the likely difference between the sample and population means regardless of the distribution of the individual data items! In particular, 68% of the time the difference between the sample and population means will be less than 1 SEM, 95% of the time the difference will be less than 2 SEMs, and so on. You can see why the result is central to statistical practice. It lets us ignore the distribution of individual data values when talking about the behavior of sample means in large samples. The distribution of individual data values becomes irrelevant when making statements about the difference between sample and population means. From a statistical standpoint, sample means obtained by replicating a study can be thought of as individual observations whose standard deviation is equal to the SEM.

Let's stop and summarize: When describing the behavior of individual values, the normal distribution can be used only when the data themselves follow something close to a normal histogram. When describing the difference between sample and population means based on large enough samples, the normal distribution can be used whatever the histogram of the individual observations. Let's continue…

Anyone familiar with mathematics and limit theorems knows that limit theorems begin, "As the sample size approaches infinity . . ." No one has infinite amounts of data. The question naturally arises about the sample size at which the result can be used in practice. Mathematical analysis, simulation, and empirical study have demonstrated that for the types of data encountered in the natural and social sciences (and certainly almost any response measured on a continuous scale) sample sizes as small as 30 to 100 (!) will be adequate.

To reinforce these ideas, consider dietary intake, which tends to follow a normal distribution. Suppose we find that daily caloric intakes in a random sample of 100 undergraduate women have a mean of 1800 kcal and a standard deviation of 200 kcal. Because the individual values follow a normal distribution, approximately 95% of them will be in the range (1400, 2200) kcal . The Central Limit theorem lets us do the same thing to estimate the (population) mean daily caloric intake of all undergraduate women. The SEM is 20 (=200/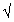100). A 95% confidence interval for the mean daily caloric intake of all undergraduate women is (1760, 1840) kcal . That is, we are 95% confident the mean daily caloric intake of all undergraduate women falls in the range (1760, 1840) kcal.

Consider household income, which invariably is skewed to the right. Most households have low incomes while a few have very large incomes. Suppose household incomes measured in a random sample of 400 households have a mean of $10,000 and a SD of $3000. The SEM is $150 (= 3000/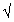 400). Because the data do not follow a normal distribution, there is no simple rule involving the sample mean and SD that can be used to describe the location of the bulk of the individual values. However, we can still construct a 95% confidence interval for the population mean income as  or $(9700, 10300). Because the sample size is large, the distribution of individual incomes is irrelevant to constructing confidence intervals for the population mean.

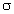• In most textbooks, the discussion of confidence intervals begins by assuming the population standard deviation, , is known. The sample and population means will be within 2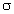/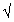n of each other, 95% of the time. The reason the textbooks take this approach is that the mathematics is easier when 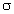is known. In practice, the population standard deviation is never known. However, statistical theory shows that the results remain true when the sample SD, s, is used in place of the population SD, .
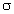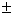• There is a direct link between having 95% confidence and adding and subtracting 2 SEMs. If more confidence is desired, the interval must be made larger/longer/wider. For less confidence, the interval can be smaller/shorter/narrower. In practice, only 95% confidence intervals are reported, although on rare occasions,  90% ( 1.645 SEM) or 99% ( 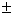2.58 SEM) confidence intervals may appear. The reason 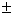2 SEMs gives a 95% CI and 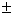2.58 SEMs gives a 99% CI has to do with the shape of the normal distribution. You can study the distribution in detail, but in practice, it's always going to be 95% confidence and 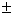2 SEM.
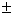• 2 SEM is a commonly used approximation.  The exact value for a 95% confidence interval based on the Normal distribution is 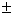1.96 SEM rather than 2, but 2 is used for hand calculation as a matter of convenience.  Computer programs use a value that is close to 2, but the actual value depends on the sample size, as we shall see.

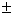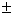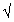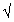A question commonly asked is whether summary tables should include mean SD or mean SEM. In many ways, it hardly matters. Anyone wanting the SEM merely has to divide the SD by n. Similarly, anyone wanting the SD merely has to multiply the SEM by n.

The sample mean describes both the population mean and an individual value drawn from the population. The sample mean and SD together describe individual observations. The sample mean and SEM together describe what is known about the population mean. If the goal is to focus the reader's attention on the distribution of individual values, report the mean 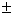SD. 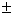If the goal is to focus on the precision with which population means are known, report the mean SEM.