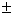 2*250/
2*250/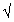 100].
100].
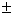 2*250].
2*250]. Other Intervals
Confidence intervals are interval estimates of population parameters. There are other types of intervals that are used for other purposes.
If confidence intervals describe where population parameters are likely to be found, what intervals describe the individuals in the population? For example, suppose we interview a sample of 100 Boston area, male, full-time college freshman find that their daily dietary intakes have a mean of 2100 kcal, a standard deviation of 250 kcal, and roughly follow a normal distribution.
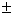 2*250/
2*250/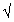 100].
100].
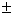 2*250].
2*250]. But, what are some of the other things we might like to say about the population?
At first blush, these appear to be the same question AND it might seem as though both of these questions can be answered by the second interval--the sample mean plus or minus two standard deviations. In many cases, this won't be too far from the truth, but there are problems with this solution.
The sample mean plus or minus a multiple of the standard deviation would work except for one (two?) things: the sample mean (standard deviation) is not equal to the population mean (standard deviation). Suppose the population standard deviation were known. The population mean plus or minus two SDs contains 95% of the population. But now slide the interval to the right, say, mimicking what happens when it is centered around the sample mean. The interval now includes more of the right tail of the population, but it loses a lot more from the left tail. That is, the sample mean plus or minus two SDs will contain less than 95% of the population.
Prediction Intervals are used to estimate the value of the next observation. They are like confidence intervals in that they are a way of generating intervals with the desired property. That is, 95% of 95% prediction intervals will contain the next observation. However, they are not probability statements because they are made after some of the data have been observed. They are not bet worthy the same way confidence intervals are not betworthy.
Since the sample mean,  , and next observation, x*, are
independent, the standard error of their difference is estimated as
, and next observation, x*, are
independent, the standard error of their difference is estimated as



Tolerance Intervals are used to estimate where a portion of a population is located. An example of a tolerance interval is "We have 90% confidence that at least 95% of the population of all total cholesterol levels are between 184 and 256 mg/dL." Notice that there are two figures associated with the interval. One is the fraction of the population that it contains, in this case at least 95%. The other is the degree of confidence we have that the interval contains that fraction, in this case 90%.
Tolerance intervals typically assume an underlying normal distribution or are nonparametric, based on the order statistics. There are tables of values that can be used to construct the actual interval.