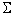 nij.
nij.
Multi-Factor Analysis of Variance
Gerard E. Dallal, Ph.D.
With only a slight exaggeration, if you understand two-factor analysis of variance, you understand all of multi-factor analysis of variance. If you understand the issues raised by analyzing two factors simultaneously, then you'll understand the issues regardless of the number of factors involved.
With two-factor analysis of variance, there are two study factors (we'll call them factor A with a levels and factor B with b levels) and we study all (a times b) combinations of levels. For example, in a diet and exercise study, DIET and EXERCISE are the two study factors and we study all combinations of DIET and EXERCISE. The data can be displayed in a two-way table like a contingency table except that each cell might contain a mean, standard deviation, and sample size.
The secret to mastering two-factor analysis of variance is to understand the underlying model. The principal reason why multi-factor analyses are interpreted incorrectly is that users do not understand what is meant by the seductively named main effect. A main effect is the effect of a particular factor on average. For example, the main effect of diet is the effect of diet averaged over all forms of exercise. Main effects are important, but focusing on them alone makes it possible to relive a series of bad jokes, namely, "The person who had his feet in the icebox and his head in the oven but was fine, on average" or "The person who drowned in a pool that was 2 feet deep, on average".
In a multi-factor analysis of variance, we look at interactions along with main effects. Interactions are the extent to which the effects of one factor differs according to the levels of another factor. If there is an interaction between DRUG and SEX, say, the drug that is best for men might be different from the one that is best for women. If there is no interaction between the factors, then the effect of one factor is the same for all levels of the other factor. With no interaction, the drug that is best on average is the best for everyone.
When a computer program reports that the main effect of drug is highly statistically significant, it is tempting to stop right there, write it up, and send off a manuscript immediately. As we've just seen, an analysis should begin with an examination of the interactions because the interpretation of the main effects changes according to whether interactions are present. However, every computer package tempts us to look at main effects first by listing them in the output before the interactions.
Let
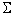 nij.
nij.
The model could be written as
 ij +
ij + 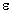 ijk
ijk but it is usually written in a different way that takes advantage of the special structure of the study.
 +
+
 i +
i +  j + (
j + (
 )ij +
)ij + 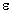 ijk
ijk where
 is an overall effect,
is an overall effect,
 i is the main effect of the i-th level of factor A,
i is the main effect of the i-th level of factor A,
 j is the main effect of the j-th level of factor B, and
j is the main effect of the j-th level of factor B, and

 )ij is an interaction, an effect unique to the particular combination of levels. The combination (
)ij is an interaction, an effect unique to the particular combination of levels. The combination (
 ) to be read as a single symbol. It is called the two factor interaction (or first order interaction) between A and B. In computer models and output, it is denoted AB or A*B. It is not the product of
) to be read as a single symbol. It is called the two factor interaction (or first order interaction) between A and B. In computer models and output, it is denoted AB or A*B. It is not the product of  i and
i and  j, which would be written
j, which would be written  i
i j.
j.
Using (
 )ij rather than a new
symbol such as
)ij rather than a new
symbol such as  ij
allows the notation to represent many factors in a convenient manner. In
a study involving four factors, there are four main effects, six two-
factor interactions, four three-factor interactions, and a four-factor
interaction. Sixteen unique symbols would be required to represent all
of the effects and the underlying model would be difficult to read. On
the other hand (
ij
allows the notation to represent many factors in a convenient manner. In
a study involving four factors, there are four main effects, six two-
factor interactions, four three-factor interactions, and a four-factor
interaction. Sixteen unique symbols would be required to represent all
of the effects and the underlying model would be difficult to read. On
the other hand (

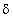 )ijl is easily understood to be the
three-factor interaction between factors A, B, and D.
)ijl is easily understood to be the
three-factor interaction between factors A, B, and D.
A model without interactions is simpler to write and easier to explain. That model is said to be additive because the individual effects of the two factors are added together to describe their joint effect. The effect of a particular level of factor A is the same whatever the level factor B and vice-versa. The difference between two levels of factor A is the same for all levels of factor B. For example, If we focus on level i of factor A, the expected responses at levels 3 and 5 of factor B are
 +
+  i +
i +  3
3 +
+  i +
i +  5
5The effect of the level of factor B is added on to the effect of level i of factor A. The difference between the expected values is
 3 -
3 -
 5
5
When interactions are present, the effect of factor A depends on the level of factor B and the effect of factor B depends on the level of factor A. With interactions, the expected values become
 +
+  i +
i +  3 + (
3 + (
 )i3
)i3  +
+  i +
i +  5 + (
5 + (
 )i5
)i5 The difference between them is
 3 + (
3 + (
 )i3] -
[
)i3] -
[ 5 + (
5 + (
 )i5]
)i5]
This difference depends on the value of i. The difference changes according to the level of factor A.
Just as with single factor ANOVA there are more parameters than groups, only more so! Constraints must be placed on the parameters so they can be estimated. The usual constraints force the parameters to sum to 0 in various ways.
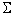
 i = 0
i = 0
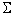
 j = 0
j = 0
 for all i
for all i
 for all j
for all j
Virtually every statistical software package displays its output starting with main effects followed successively more complicated interactions, that is, first come the two-factor interactions, then the three-factor interactions, and so on. However, the evaluation of a multi-factor analysis of variance should proceed in the opposite order, that is, by first looking at the most complicated interaction and, if it can be dismissed, by successively less complicated interactions. The underlying principle behind the analysis stated in its most dramatic form is: Never analyze main effects in the presence of an interaction. More properly, the principle is "never analyze an effect without regard to the presence of higher order relatives" but this lacks some of the dramatic bite of the first statement.
The reasons for this advice (and an understanding of when it can be safely ignored!) is easily obtained from a close examination of the model. The test for interaction asks whether the row effects are constant across the columns and, equivalently, whether the column effects are constant across the rows. If this is true--that is, if there is no interaction--then the model has been simplified dramatically. It makes sense to talk about row effects because they are the same for all columns. A similar argument applies regarding column effects.
Regardless of whether interactions are present, the test of row effects tests whether there is a common mean response for each row after averaging across all columns--that is, the test for row effects tests the hypothesis

In similar fashion, the test of column effects tests whether there is a common mean response for each column after averaging across all rows--that is, the test for column effects tests the hypothesis

If there is no interaction in the model, it makes sense to look for global (or overall or simple) row effects since they describe the differences between row levels regardless of the column level. Similarly, for column effects.
If interaction is present in the model, it doesn't make sense to talk about simple row effects because the row effects are column specific. For example, suppose the rows represent two drugs (X and Y) and the columns represent the sex of the subject. Suppose X is ineffective for both men and women while Y is ineffective for men but helps women. There is a drug-by-sex interaction since the difference between the drug changes with sex. The simple drug effect says that Y is better than X on average, that is, the hypothesis

will be rejected even though both drugs are ineffective for men because Y is effective for women. The main effects look at whether the drugs behave the same when their effect is averaged over both men and women. When averaged over both men and women, the effect is not the same. Thus, the result of testing main effect is likely to be irrelevant since it doesn't apply equally to men and women. When an interaction is present, it is usually a mistake to report an analysis of the main effects because the effects will either be irrelevant or be misinterpreted as applying equally to everyone. Hence, the maxim Never analyze main effects in the presence of an interaction.
I would prefer to leave it at that--Never analyze main effects in the presence of an interaction--because it's the right advice in almost every case. There are two exceptions worth mentioning. I hesitate only because it might make the general rule seem less important than it is.
The first exception has to do with the distinction between statistical significance and practical importance. It is quite possible for an interaction to be statistically significant yet not large enough to blur the message of the main effects. For example, consider two cholesterol lowering drugs. Suppose both are effective and while drug X has the same effect on men and women, drug Y on average lowers cholesterol an additional 10 mg/dl in men and 5 mg/dl in women. There is a drug-by-sex interaction because the difference between the drugs is not the same for men and women. Yet, the message of the main effects--take drug Y--is unaffected by the interaction.
The second exception comes from a hand-written note to myself on a scrap of paper I found in one of my files. (Perhaps someone can provide me with the original source if it wasn't something I concocted on the spur of the moment. It must be from a few years ago, because the page makes reference to SPSS-X.) The note reads, "Recall story of dairy farmer who could use only one type of feed for all breeds in herd." The story must go something like this...
A dairy farmer wished to determine which type of feed will produce the greatest yield of milk. From the research literature she is able to determine the mean milk output for each of the breeds she owns for each type of feed she is considering. As a practical matter, she can use only one type of feed for her herd.
Since she can use only one type of feed, she wants the one that will produce the greatest yield from her herd. She wants the feed type that produces the greatest yield when averaged over all breeds, even if it means using a feed that is not optimal for a particular breed. (In fact, it is easy to construct examples where the feed-type that is best on average is not the best for any breed!) The dairy farmer is interested in what the main effects have to say even in the presence of the interaction. She wants to compare

where the means are obtained by averaging over breed.
For the sake of rigor, it is worth remarking that this assumes the herd is composed of equal numbers of each breed. Otherwise, the feed-types would be compared through weighted averages with weights determined by the composition of the herd. For example, suppose feed A is splendid for Jerseys but mundane for Holsteins while feed B is splendid for Holsteins but mundane for Jerseys. Finally, let feed C be pretty good for both. In a mixed herd, feed C would be the feed of choice. If the composition of the herd were to become predominantly Jerseys, A might be the feed of choice with the gains in the Jerseys more than offsetting the losses in the Holsteins. A similar argument applies to feed B and a herd that is predominantly Holsteins.